円管、三角形管、正方形管の圧力損失低減と伝熱劣化の比較、乱流エネルギーおよび二次流れの効果
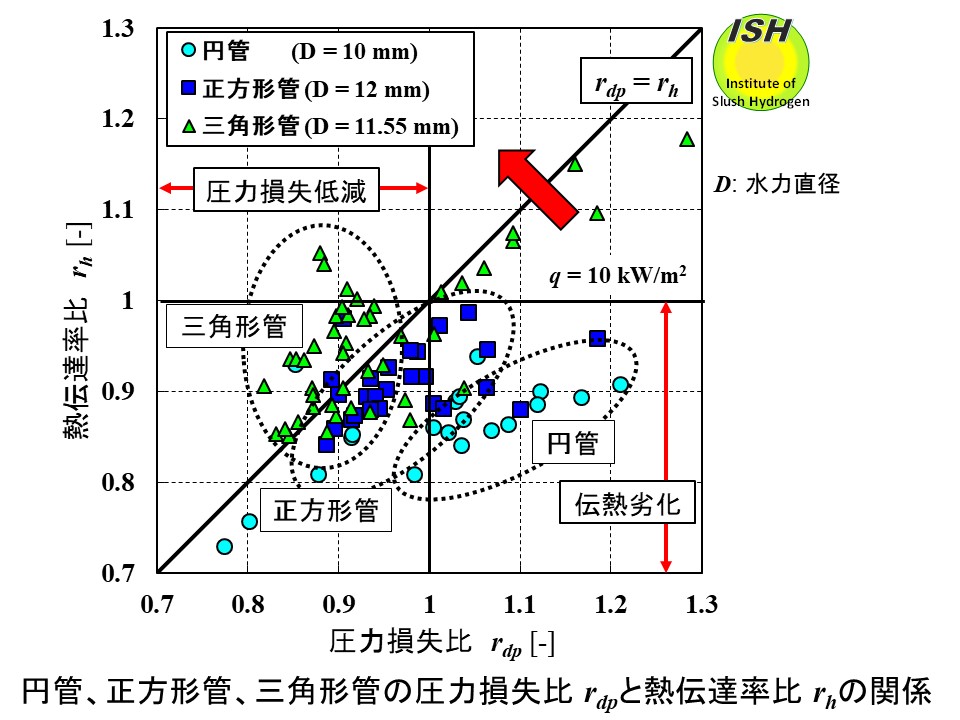
熱流束 10 kW/m2 において円管(内径 10 mm)、正方形管(一辺 12 mm)、上向き正三角形管(一辺 20 mm)から得られた同一流速における 圧力損失比
rdp と熱伝達率比 rh の相関関係を上図に示す [7, 24]。rdp、rh は液体窒素の圧力損失、熱伝達率を基準にしたスラッシュ窒素の圧力損失比、熱伝達率比である。3種類の管の水力直径 D は同程度である。
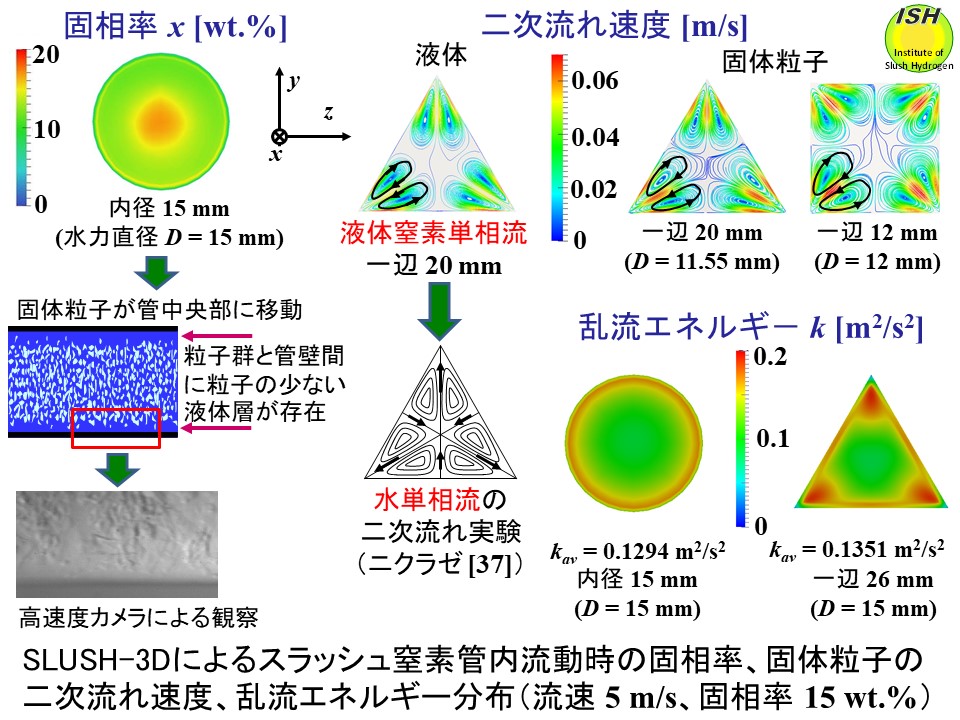
円管の最大低減量、最大劣化量は前述のように三角形管より大きいが、三角形管の rh は、 円管、正方形管と比べると rdp よりも大きい傾向を示す(rh > rdp )。理由として次のことが考えられる。熱流束 0 kW/m2 における円管(内径 15 mm)、同じ水力直径をもつ三角形管(一辺 26 mm、D=15 mm)の乱流エネルギー分布を、開発した三次元流動・伝熱数値解析プログラム(SLUSH-3D)で解析した結果を下図に示す(”スラッシュ数値解析、SLUSH-3D”のページ参照)。水力直径が同じ場合、頂点で発生する乱流エネルギーの影響により三角形管の方が円管よりも平均乱流エネルギーが大きくなる。従って、三角形管(一辺
20 mm、D=11.55 mm)と内径 10 mm円管の比較においても三角形管の平均乱流エネルギーが大きく、三角形管の圧力損失低減効果、熱伝達劣化*が乱流エネルギーにより抑制され、円管の方が圧力損失比と熱伝達率比が共に小さくなる(低減、劣化効果が大)。
さらに、三角形管の場合でも円管と同様に大部分の固体窒素粒子は下図に示す乱流エネルギーの小さい管中央部を流動するので3つの頂点付近には固体窒素粒子の少ない液体層が多く存在する。また、下図に示すように頂点付近から管壁に沿って固体窒素粒子および液体窒素の第二種二次流れ(円管では出現しない)が存在するので管壁付近の加熱された液体が管中央部へ拡散され三角形管では伝熱が促進される(rh > rdp)。SLUSH-3Dに非線形渦粘性(non-lineark-ε)モデルを使用して三角形管および正方形管内の液体窒素、固体窒素粒子の第二種二次流れを再現している。非加熱時の液体窒素単相流の第二種二次流れの数値解析結果はニクラゼ(Nikuradse)の有名な水の実験結果
[37]と良く一致することを事前に検証している。
正方形管でも下図に示すように第二種二次流れが同様に存在し、数値解析結果では平均乱流エネルギーは三角形管と円管の中間の値である [7, 22, 24]。正方形管では4個の頂点付近に存在する液体層が三角形管よりも少なく液体層の影響が小さいので三角形管と円管の中間の特性を示す
[23]。
伝熱劣化は一般には好ましくないので、スラッシュ流体の伝熱管設計において圧力損失、熱伝達のいずれが重要かにより管断面形状を選定することになる。スラッシュ水素のみを輸送する長距離配管ではポンプ動力を低減する点から圧力損失低減が大きい円管が適しており、高温超伝導送電用の冷媒配管にはクエンチ伝播防止のため伝熱特性も考慮した断面形状(円管、矩形管)を選定すること、熱交換器には三角形管のように伝熱劣化の小さい断面形状を選定することが設計上有用となる。また、固体粒子径を調整することにより、圧力損失低減量をある程度保持しつつ熱伝達劣化量を小さく保持することが可能であり、断面形状とは関係なく用途に応じてスラッシュ流体のメリットを生かすことができる。
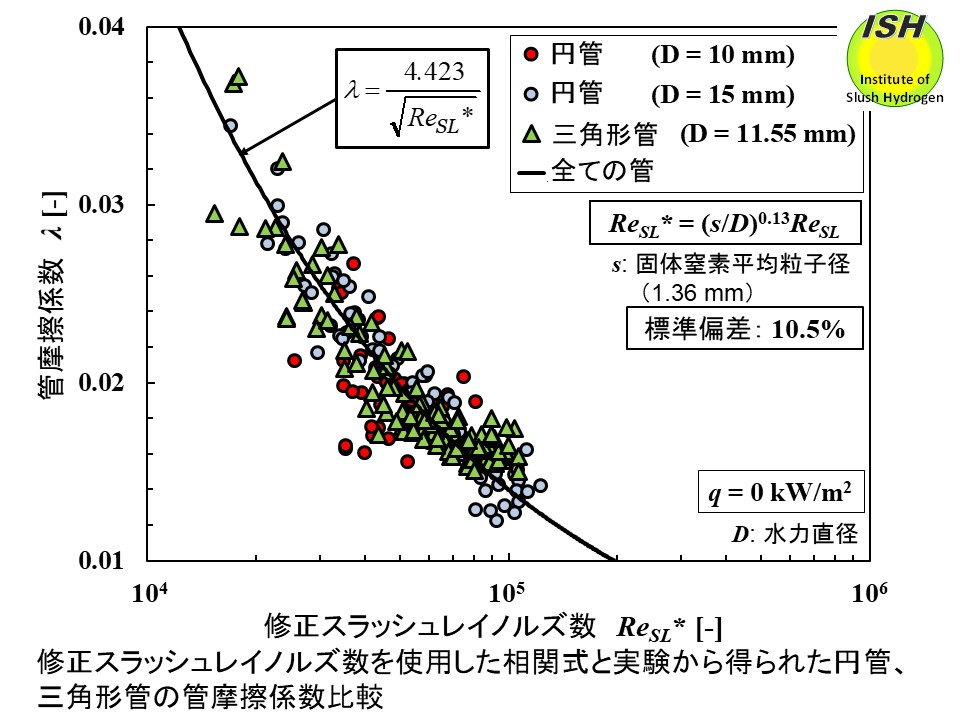
円管では μSL=μL [1-(x /0.6)]-1.8 で表されるみかけの粘性係数 μSL [33] を用いたスラッシュRe数(ReSL)を、正三角形管では液体窒素の粘性係数 μL を用いたスラッシュRe数(ReSL)を使用して、修正スラッシュレイノルズ数 ReSL*=(s /D )0.13ReSL を定義する。ここで、s は固体窒素の平均粒子径(1.36 mm)、D は水力直径である。円管、正三角形管の圧力損失データをもとに ReSL*と管摩擦係数 λ の関係式を最小自乗法により求めると、下図に示すように、流速と体積固相率 x から圧力損失低減を考慮した円管と正三角形管の両方の管摩擦係数を一つの式で精度良く予測できる [7, 24]。ポンプ動力を推定する際に、工学上非常に有用である。
* 圧力損失低減、伝熱劣化メカニズム:加熱時、非加熱時共に、摺動流、非均質流を経て擬均質流(均質流)となる高流速時には、管中央部に移動した固体粒子群によって管壁での乱流発達が抑制され、圧力損失低減が発生する
[20]。一方、熱伝達は管壁付近の固体粒子の少ない液体層で行われるが管壁での乱流発達が抑制されるので管壁付近の加熱された液体が管中央部へ拡散する作用が抑制され、熱伝達劣化が発生する
[21]。